Floyd Warshall Algorithm
Graph
Floyd's or Floyd-Warshall Algorithm is used to find all pair shortest path for a graph. This algorithm works for weighted graph having positive and negative weight edges without a negative cycle.
Problem
Consider the following weighted graph. 
Our task is to find the all pair shortest path for the given weighted graph.
Steps
Step 1: Remove all the loops.
Note! Any edge that starts and ends at the same vertex is a loop.

Step 2: Remove all parallel edges between two vertices leaving only the edge with the smallest weight.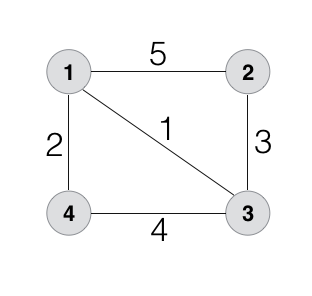
Step 3: Create a distance and sequence table.
How we will proceed
- To find the shortest path between any two nodes we will draw two tables namely, Distance Table (D) and Sequence Table (S).
- We can also refer these tables as matrix.
- The Distance table (D) will hold distance between any two vertices.
- The Sequence table (S) will hold the name of the vertices that will help in finding the shortest path between any two vertices.
- If a graph has k vertices then our table D and S will have k rows and k columns.
- We will use the iterative method to solve the problem.
Notations we will be using
k = Iteration number
Dk = Distance table in kth iteration
Sk = Sequence table in kth iteration
dij = The distance between vertex i and j
There are 4 vertices in the graph so, our tables (Distance and Sequence) will have 4 rows and 4 columns.
Distance table D
This table holds the weight of the respective edges connecting vertices of the graph. So, if there in an edge u --> v connecting vertex u to vertex v and having weight w then we will fill the distance table D[u][v] = w. If there is no edge connecting any two vertex u to v then in that case we will fill D[u][v] = INFINITY.
| D0 | 1 | 2 | 3 | 4 |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |
From the graph above we will get the following distance table.
| D0 | 1 | 2 | 3 | 4 |
| 1 | - | 5 | 1 | 2 |
| 2 | 5 | - | 3 | INF |
| 3 | 1 | 3 | - | 4 |
| 4 | 2 | INF | 4 | - |
INF means INFINITY
Sequence table S
This table holds the vertex that will be used to find the shortest path to reach from vertex u to vertex v.
| S0 | 1 | 2 | 3 | 4 |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |
From the graph above we will get the following sequence table.
| S0 | 1 | 2 | 3 | 4 |
| 1 | - | 2 | 3 | 4 |
| 2 | 1 | - | 3 | 4 |
| 3 | 1 | 2 | - | 4 |
| 4 | 1 | 2 | 3 | - |
INF means INFINITY
Important Condition
We will fill the cell Cij in distance table Dk using the following condition.
Is dij > dik + dkj [in distance table Dk-1]
If YES then fill the cell Cij in Dk table with the value dik + dkj of Dk-1 table
If NO then fill the cell Cij in Dk table with the value dij of Dk-1 table
where
i = row number
j = column number
k = iteration number
i.e., we will always fill the cell Cij in Dk table with the smallest value.
Note! If a graph has N vertices then we will be iterating N times.
The graph has 4 vertices so, we will be iterating 4 times.
Solution
After completing the 4 iterations we will get the following distance array.
| D4 | 1 | 2 | 3 | 4 |
| 1 | - | 4 | 1 | 2 |
| 2 | 4 | - | 3 | 6 |
| 3 | 1 | 3 | - | 3 |
| 4 | 2 | 6 | 3 | - |
And the following sequence table
| S4 | 1 | 2 | 3 | 4 |
| 1 | - | 3 | 3 | 4 |
| 2 | 3 | - | 3 | 3 |
| 3 | 1 | 2 | - | 1 |
| 4 | 1 | 3 | 1 | - |
And the required shortest paths.
| Source Vertex (i) | Destination Vertex (j) | Distance | Shortest Path |
| 1 | 2 | 4 | 1 --> 3 --> 2 |
| 1 | 3 | 1 | 1 --> 3 |
| 1 | 4 | 2 | 1 --> 4 |
| 2 | 3 | 3 | 2 --> 3 |
| 2 | 4 | 6 | 2 --> 3 --> 1 --> 4 |
| 3 | 4 | 3 | 3 --> 1 --> 4 |
Code in C
#include <stdio.h>
#define INF 99999
#define MAX 10
void display(int arr[][MAX], int size);
void floyds(int D[][MAX], int S[][MAX], int size);
int main(void) {
//distance array
/*
we have created a distance array of size 10x10 (MAX x MAX)
but we will be using only 4x4 as the graph has 4 vertices
*/
int D[MAX][MAX] = {
{INF, 5, 1, 2},
{5, INF, 3, INF},
{1, 3, INF, 4},
{2, INF, 4, INF}
};
//sequence array
/*
we have created a sequence array of size 10x10 (MAX x MAX)
but we will be using only 4x4 as the graph has 4 vertices
*/
int S[MAX][MAX] = {
{INF, 2, 3, 4},
{1, INF, 3, 4},
{1, 2, INF, 4},
{1, 2, 3, INF}
};
int size = 4; //total number of vertices in the graph
floyds(D, S, size);
return 0;
}
void floyds(int D[][MAX], int S[][MAX], int size) {
int i, j, k, l;
//arrays to hold data for current iteration
/*
we have created arrays of size 10x10 (MAX x MAX)
but we will be using only 4x4 as the graph has 4 vertices
*/
int Dk[MAX][MAX], Sk[MAX][MAX];
//set Dk and Sk to 0
for(i = 0; i < size; i++) {
for(j = 0; j < size; j++) {
if(i == j) {
Dk[i][j] = INF;
Sk[i][j] = INF;
} else {
Dk[i][j] = 0;
Sk[i][j] = 0;
}
}
}
//iteration
/*
since array indexing start from 0 in C programming
so, we are setting i,j,k,l to 0
note! in the video tutorial above we have used arrays
starting from index 1
video: https://www.youtube.com/watch?v=X6n30V6qCWU
*/
for(k = 0; k < size; k++) {
//step 1:
//for each iteration we copy the kth row and kth column to
//the current array
for(l = 0; l < size; l++) {
//copy row
Dk[k][l] = D[k][l];
Sk[k][l] = S[k][l];
//copy column
Dk[l][k] = D[l][k];
Sk[l][k] = S[l][k];
}
//step 2:
//compute the distance and sequence value for
//current iteration
for(i = 0; i < size; i++) {
//for kth iteration we skip the kth row
if(i == k) {
continue;
}
for(j = 0; j < size; j++) {
//for kth iteration we skip the kth column
if(j == k) {
continue;
}
//if i and j are same i.e., referring to same vertex we skip it
if(i == j) {
continue;
}
//checking
if(D[i][j] > D[i][k] + D[k][j]) {
Dk[i][j] = D[i][k] + D[k][j];
Sk[i][j] = (k+1); //kth iteration, as indexing starts from 0 so, we add 1
} else {
Dk[i][j] = D[i][j];
Sk[i][j] = S[i][j];
}
}
}
//step 3:
//copy content of Dk and Sk to D and S
for(i = 0; i < size; i++) {
for(j = 0; j < size; j++) {
D[i][j] = Dk[i][j];
S[i][j] = Sk[i][j];
}
}
}
//print the distance array and sequence array result
printf("Distance array: \n");
display(D, size);
printf("Sequence array: \n");
display(S, size);
}
void display(int arr[][MAX], int size) {
int i, j;
for(i = 0; i < size; i++) {
for(j = 0; j < size; j++) {
if(arr[i][j] == INF) {
printf("%10s ", "INF");
} else {
printf("%10d ", arr[i][j]);
}
}
printf("\n");
}
}
Time complexity
The time complexity of Floyd's or Floyd-Warshall algorithm is O(V3).
ADVERTISEMENT