Dijkstra Algorithm - Finding Shortest Path - Graph - dyclassroom

In this tutorial we will learn to find shortest path between two vertices of a graph using Dijkstra's Algorithm.

Graph

Consider the following graph.

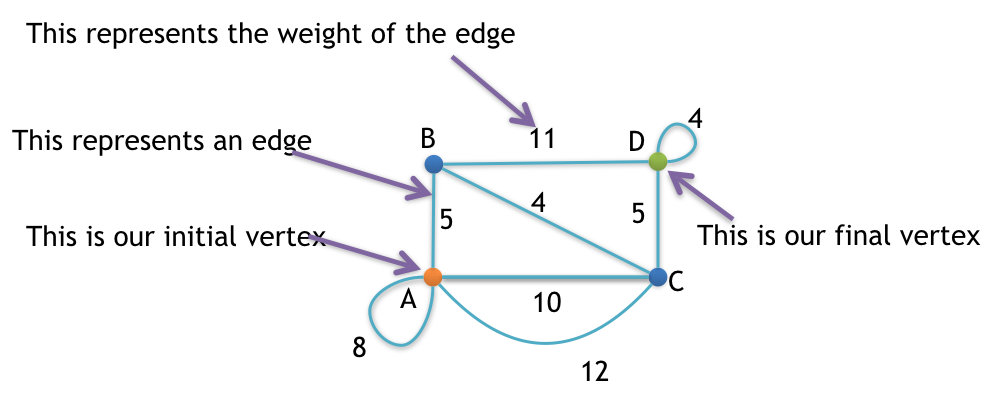
Steps

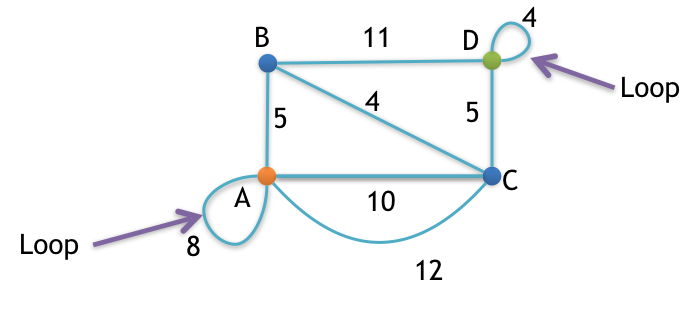
Step 1: Remove all loops

Any edge that starts and ends at the same vertex is a loop.

Loops are marked in the image given below.

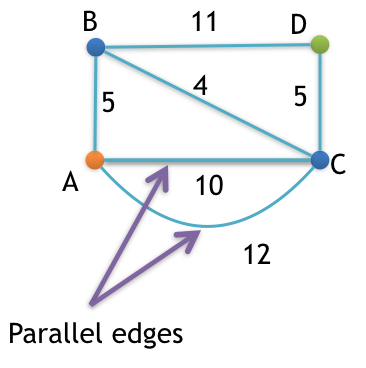
Step 2: Remove all parallel edges between two vertex except the one with least weight

In this graph, vertex A and C are connected by two parallel edges having weight 10 and 12 respectively. So, we will remove 12 and keep 10.

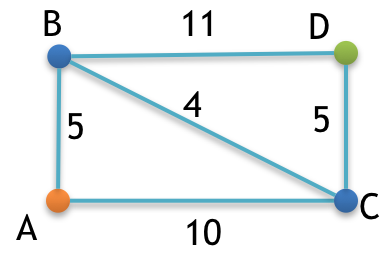
We are now ready to find the shortest path from  vertex A to vertex D.

Step 3: Create shortest path table

As our graph has 4 vertices, so our table will have 4 columns.

Note! Column name is same as the name of the vertex.

After solving this we will have the following result. (See the above video for the steps)

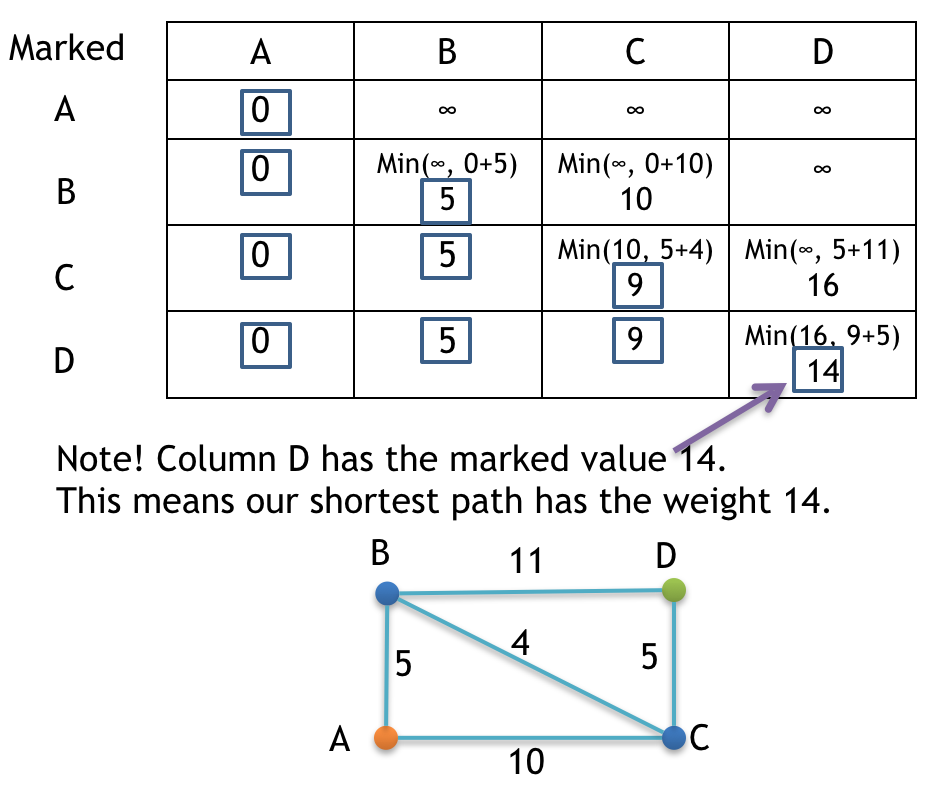
Result

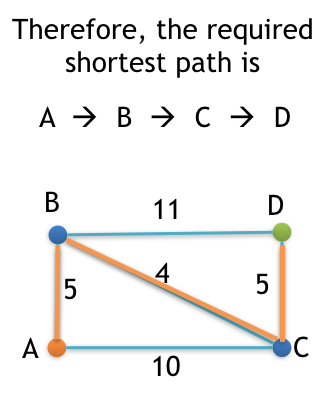
Following is the required shortest path

Code

Note! In the given code we are representing Vertices using decimal numbers.
So,
vertex A is denoted by digit 0.
vertex B is denoted by digit 1.
vertex C is denoted by digit 2.
vertex D is denoted by digit 3.

/**
 * file: dijkstra.c
 * author: yusuf shakeel
 * date: 2014-03-03
 *
 * description: find shortest path betweem two vertices
 *
 * vertices are represented using numbers.
 * vertex A becomes 0
 * vertex B becomes 1
 * and so on...
 */

#include <stdio.h>
#include <stdlib.h>

/**
 * contant to represent infinity
 * it is assumed that no edge in the vertex will have weight equal
 * to this value.
 */
#define INF 9999

/**
 * total number of vertices in the graph
 */
#define V 4

/**
 * this function will return the minimum value
 */
int findMin(int x, int y) {
  if (x < y) {
    return x;
  }
  return y;
}

/**
 * this function will check if the vertex is marked
 */
int isMarked(int v, int markedVertices[], int markedVerticesIdx) {

  int i = 0;
  for (i = 0; i < markedVerticesIdx; i++) {
    if (v == markedVertices[i]) {
      return 1;
    }
  }

  return 0;
}

/**
 * this function will find shortest path between source and destination vertex
 */
void dijkstra(int graph[V][V], int src, int dest) {

  //variables
  int i, r, c,
    tmpC,
    min,
    currVertex,
    edgeWt = 0,
    destValue = 0,
    markedValue = 0,
    wtTableR = 0,
    markedVerticesIdx = 0;

  /**
   * array containing vertices in the shortest path
   */
  int shortestPathVertices[V] = {-1};
  int shortestPathVerticesIdx = 0;
  
  /**
   * this table will hold the weight
   */
  int weightTable[V][V];
  for (r = 0; r < V; r++) {
    for (c = 0; c < V; c++) {
      weightTable[r][c] = INF;
    }
  }
  weightTable[wtTableR++][src] = 0;

  /**
   * vertices that are marked
   */
  int markedVertices[V] = {-1};
  markedVertices[markedVerticesIdx++] = src;
  currVertex = src;

  /**
   * find shortest path
   */
  while(currVertex != dest) {

    /**
     * copy marked values to the next row of weightTable
     */
    for (i = 0; i < markedVerticesIdx; i++) {
      c = markedVertices[i];
      weightTable[wtTableR][c] = weightTable[wtTableR - 1][c];
    }

    /**
     * find the weight from the current vertex to all the other
     * vertices that are directly connected and not yet marked
     */
    for (c = 0; c < V; c++) {

      if (c != currVertex && !isMarked(c, markedVertices, markedVerticesIdx)) {

        edgeWt = graph[currVertex][c];
        destValue = weightTable[wtTableR - 1][c];
        markedValue = weightTable[wtTableR][currVertex];

        min = findMin(destValue, markedValue + edgeWt);

        weightTable[wtTableR][c] = min;

      }

    }

    /**
     * find minimum unmarked vertices in current row
     */
    min = INF;
    for (c = 0; c < V; c++) {

      if (!isMarked(c, markedVertices, markedVerticesIdx)) {
        if (weightTable[wtTableR][c] < min) {
          min = weightTable[wtTableR][c];
          tmpC = c;
        }
      }

    }

    /**
     * found a new vertex for marking
     */
    markedVertices[markedVerticesIdx++] = tmpC;
    currVertex = tmpC;
    
    /**
     * variables update
     */
    wtTableR++;

  }

  /**
   * compute shortest path vertices
   */
  c = dest;
  shortestPathVertices[shortestPathVerticesIdx++] = c;
  markedValue = weightTable[wtTableR - 1][dest];
  for (r = wtTableR - 2; r >= 0; r--) {

    if (weightTable[r][c] != markedValue) {
      c = markedVertices[r];
      markedValue = weightTable[r][c];
      shortestPathVertices[shortestPathVerticesIdx++] = c;
    }

  }

  /**
   * display the weight and shortest path
   */
  printf("Shortest Path between %d and %d\n", src, dest);
  for (i = shortestPathVerticesIdx-1; i >= 0; i--) {
    printf("%d", shortestPathVertices[i]);
    if (i > 0) {
      printf(" --> ");
    }
  }
  printf("\n");
  printf("Weight of the path: %d\n", weightTable[wtTableR-1][dest]);

}

int main(void) {

  /**
   * 2d array which holds the weight of the edges 
   */  
  int graph[V][V] = {
    {0, 5, 10, INF},
    {5, 0, 4, 11},
    {10, 4, 0, 5},
    {INF, 11, 5, 0}
  };

  /**
   * source and destination vertices
   */
  int src = 0;
  int dest = 3;

  /**
   * find shortest path
   */
  dijkstra(graph, src, dest);

  return 0;
}

Output

Shortest Path between 0 and 3
0 --> 1 --> 2 --> 3
Weight of the path: 14

More topics

Dijkstra Algorithm - Finding Shortest Path