Finding nth Fibonacci number

Programming

← Prev Next →

In this programming tutorial we will learn to solve Fibonacci series problems.

What is Fibonacci series?

Fibonacci series is a series of numbers (also known as Fibonacci number) such that any number is a sum of the two preceding numbers.

The first two numbers of the Fibonacci series are 1 and 1.

In the following example we have the first 10 Fibonacci numbers.

1, 1, 2, 3, 5, 8, 13, 21, 34 and 55.

Calculating Fibonacci number

If we have two Fibonacci number, lets say, 5 and 8 then, the next Fibonacci number will be 5+8 i.e. 13.

Following is the formula to calculate n^th Fibonacci number.

fib(n) = fib(n - 1) + fib(n - 2)

where, fib(0) = 0
and fib(1) = 1
and fib(2) = 1

So, if we want to calculate 3rd Fibonacci number we will write the following.

fib(3) = fib(2) + fib(1)

we know, fib(2) and fib(1) are both 1

so, fib(3) = 1 + 1
= 2

Lets try another one.

Find the 5th Fibonacci number.

fib(5) = fib(4) + fib(3)

So, to compute the 5th fibo number we must know the 4th and 3rd fibo numbers.


fib(4) = fib(3) + fib(2)


To compute the 4th fibo number we must know the 3rd and 2nd fibo numbers.

fib(3) = fib(2) + fib(1)

we know fib(2) and fib(1) both are 1

so, fib(3) = 1 + 1 = 2


using this we can write

fib(4) = fib(3) + fib(2)
= 2 + 1
= 3


therefore,
fib(5) = fib(4) + fib(3) 
= 3 + 2
= 5

So, lets write some code and solve this problem.

Simple approach

In this section we will find the nth Fibonacci number using the simple approach of adding two preceding (n-1)th and (n-2)th numbers.

We start by setting x = 1 and y = 1 where, x and y initially represent the first and second Fibonacci numbers.

The nth Fibonacci number is saved in variable ans.

We will take the value of n from the user.

Note! The value of n will be an integer value greater than or equal to 1 i.e. n >= 1.

If the value of n is greater than 2 then we will enter the if block. Otherwise, we will enter the else block.

For n <= 2 i.e. if n is 1 or 2 then we know the Fibonacci number is 1 so, we will output that.

For n > 2 we will enter the if block.

Code

C program:

#include <stdio.h>

int main(void) {

  int x = 1, y = 1, n, ans;

  scanf("%d", &n);

  if (n > 2) {

    ans = x + y;

    /** 
     * (n -= 2) line as we are adding x and y in the above line
     * this considers that we have used the first 2 numbers of
     * the Fibonacci series
     */
    n -= 2;
    
    while(n--) {

      ans = x + y;
      
      x = y;
      
      y = ans;

    }

  } else {
    
    ans = 1;

  }

  printf("Answer: %d\n", ans);

  return 0;

}

Recursion approach

In this section we will find the nth Fibonacci number using recursion.

To solve the problem recursively we use the Fibonacci number definition i.e. fib(n) = fib(n - 1) + fib(n - 2).

Note! fib(0) = 0 and fib(1) and fib(2) both are 1.

Lets say we want to find the 5th Fibonacci number then using recursion we will get the following.

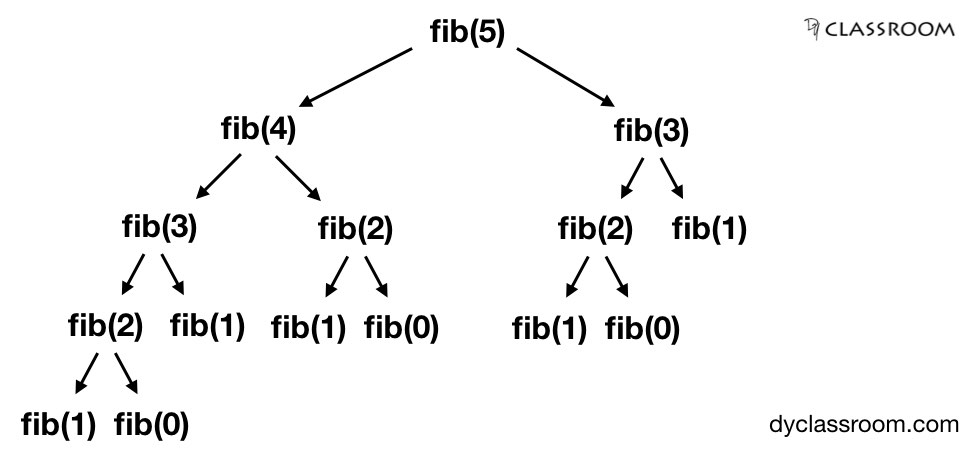
Downside of using recursion to find the nth Fibonacci number is that we calculate the same value, like fib(2) or fib(3) multiple times.

You can also check out this tutorial on Fibonacci series using recursion.

Code

And here is the recursion code written in C programming language.

#include <stdio.h>

//function declaration
int fibo(int n);

int main(){
  //variable declaration
  int n, f;
  
  //input
  printf("Enter n: ");
  scanf("%d", &n);
  
  //recursive
  f = fibo(n);
  printf("Recursive Fibo: %d\n", f);
  
  return 0;
}

//function definition
int fibo(int n){
  if(n <= 1)
    return n;
  else
    return fibo(n-1) + fibo(n-2);
}

Memoization approach

To speed up the recursion approach we can take help of memoization.

In memoization approach we save the calculated value of fib(i) for future reference thus avoiding recalculation and saving time.

So, we are trading space to again speed.

Code

Following is the C program to find nth Fibonacci number using memoization.

#include <iostream>
using namespace std;

#define MAX 10000

int fib_memoize(int n, int mem[]);

int main() {

  // creating a memory bank
  int mem[MAX+1];

  // initializing the mem
  for(int i = 0; i <= MAX; i++) {
    mem[i] = -1;
  }

  // setting some initial known values
  mem[0] = 0;
  mem[1] = 1;
  mem[2] = 1;

  // finding the result.
  cout << "fib(1) = " << fib_memoize(1, mem) << endl;
  cout << "fib(2) = " << fib_memoize(2, mem) << endl;
  cout << "fib(5) = " << fib_memoize(5, mem) << endl;
  cout << "fib(7) = " << fib_memoize(7, mem) << endl;
  cout << "fib(9) = " << fib_memoize(9, mem) << endl;
  cout << "fib(10) = " << fib_memoize(10, mem) << endl;

  return 0;
}

int fib_memoize(int n, int mem[]) {
  if (mem[n] != -1) {
    return mem[n];
  } else {
    return fib_memoize(n-1, mem) + fib_memoize(n-2, mem);
  }
}

Hope this tutorial helped. Feel free to check out other tutorials on this website. And do share this page link with your friends on social media.

See you in the next tutorial. Have fun coding.

← Prev Next →