C - Pointers and Two Dimensional Array

In this tutorial we will learn to work with two dimensional arrays using pointers in C programming language.

In the previous tutorial Pointers and One Dimensional Array we learned to work with one dimensional character array. Feel free to checkout that tutorial.

Creating a two dimensional array

To keep things simple we will create a two dimensional integer array num having 3 rows and 4 columns.

int num[3][4] = {
  {1, 2,  3,  4},
  {5, 6,  7,  8},
  {9, 10, 11, 12}
};

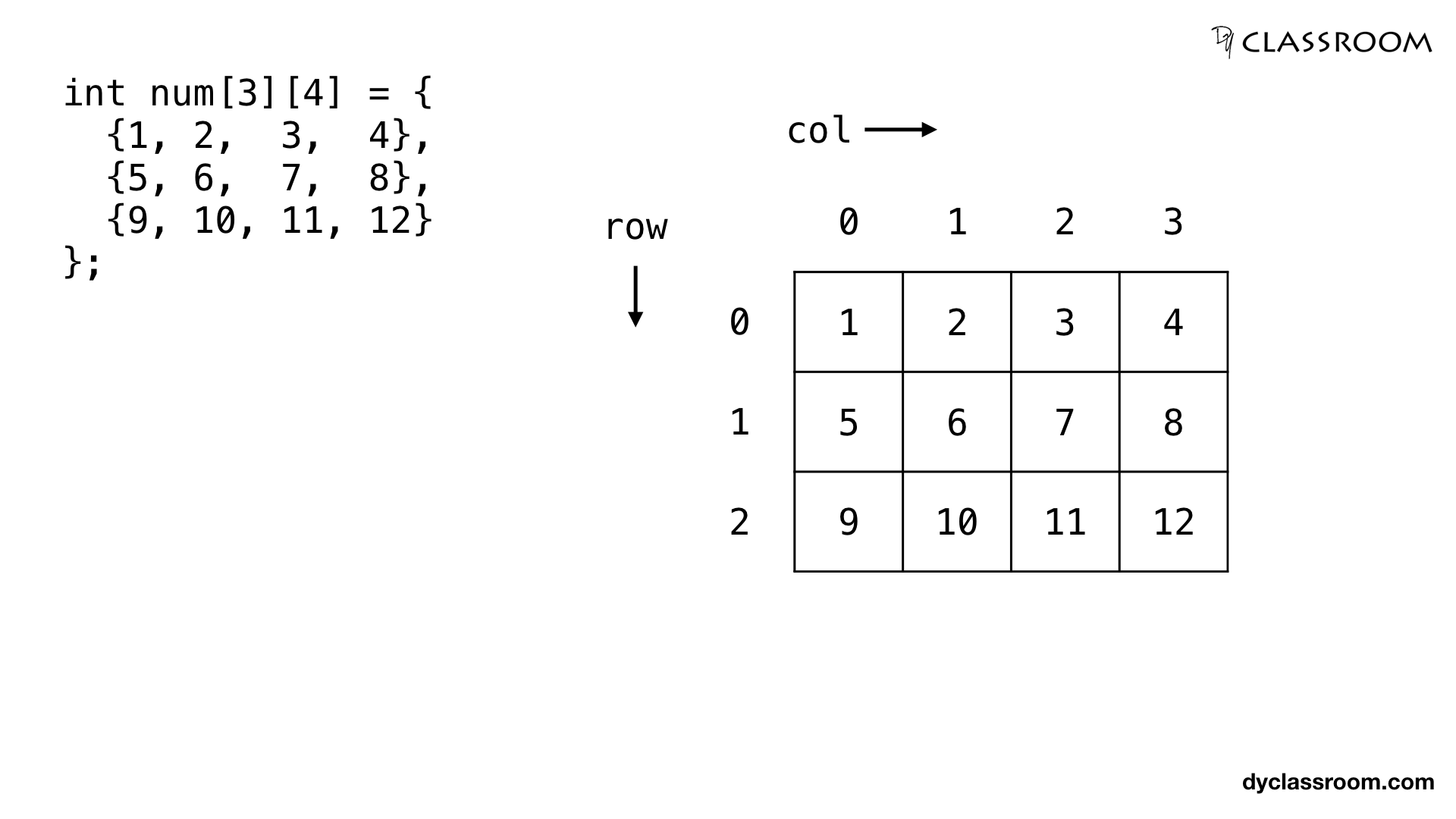
In the above image we are showing the two dimensional array having 3 rows and 4 columns.

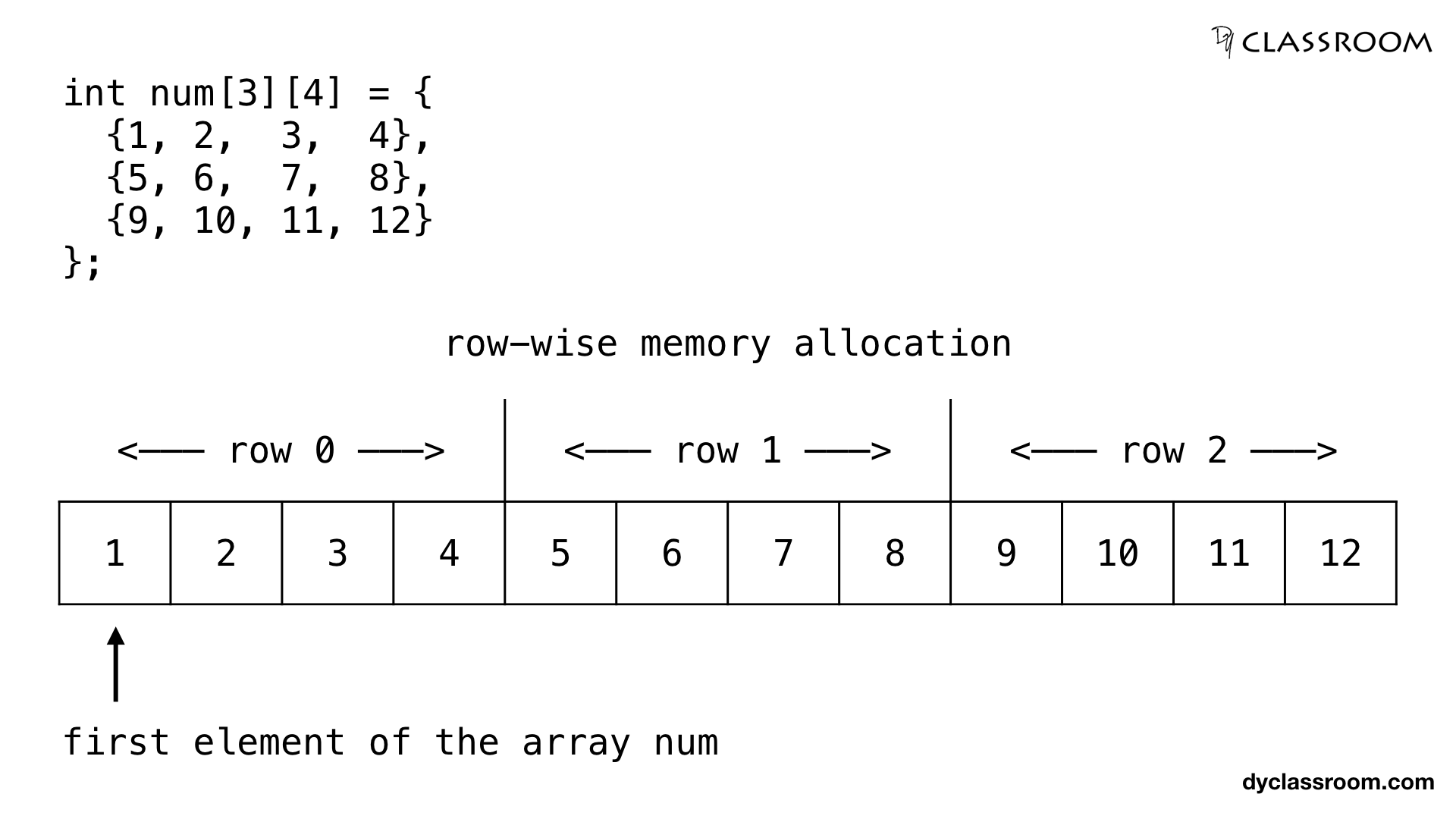
The compiler will allocate the memory for the above two dimensional array row-wise meaning the first element of the second row will be placed after the last element of the first row.

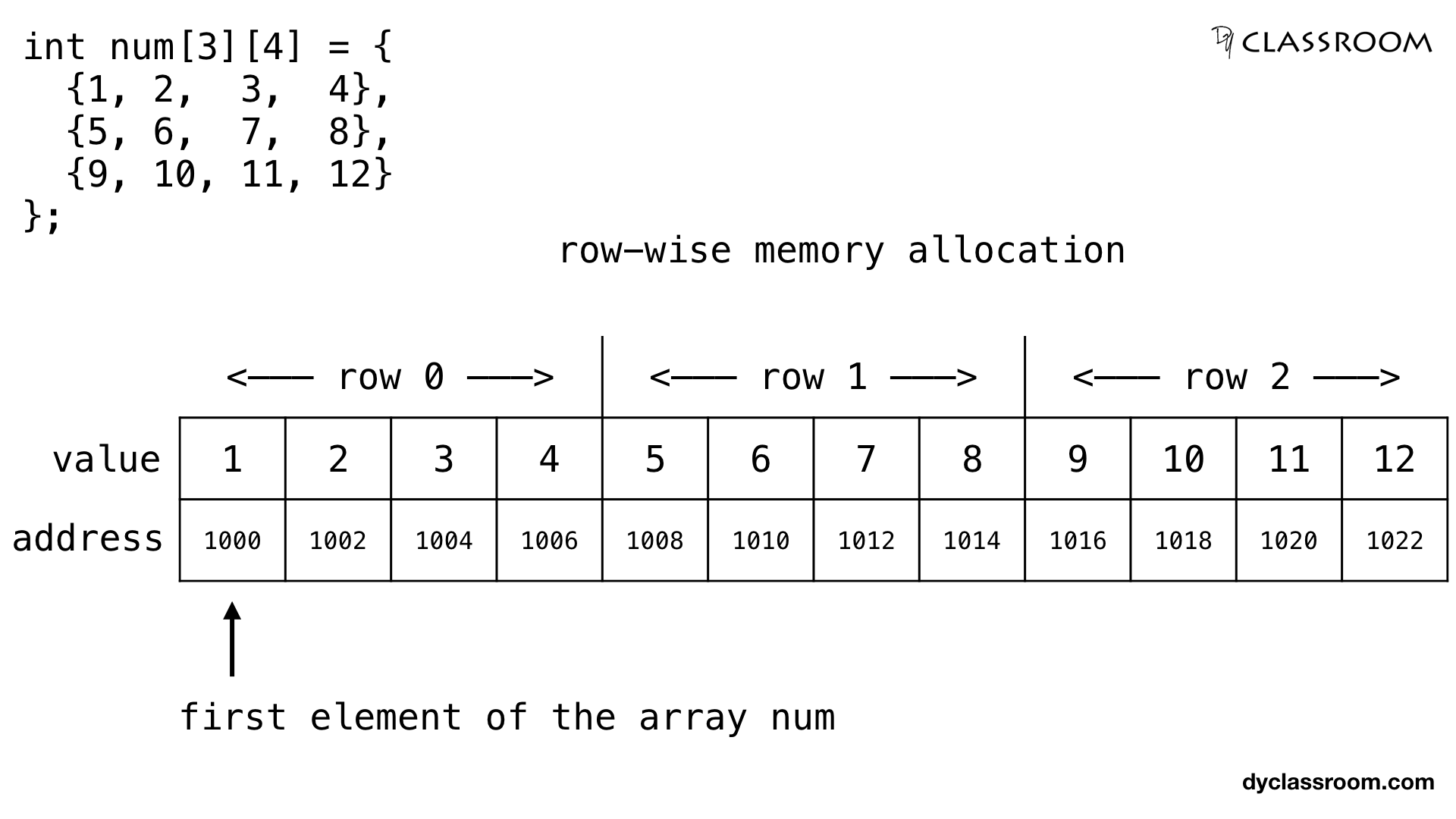
And if we assume that the first element of the array is at address 1000 and the size of type int is 2 bytes then the elements of the array will get the following allocated memory locations.

Create pointer for the two dimensional array

We have created the two dimensional integer array num so, our pointer will also be of type int.

We will assign the address of the first element of the array num to the pointer ptr using the address of & operator.

int *ptr = &num[0][0];

Accessing the elements of the two dimensional array via pointer

The two dimensional array num will be saved as a continuous block in the memory. So, if we increment the value of ptr by 1 we will move to the next block in the allocated memory.

In the following code we are printing the content of the num array using for loop and by incrementing the value of ptr.

#include <stdio.h>

int main(void) {
  
  // 2d array
  int num[3][4] = {
    {1, 2,  3,  4},
    {5, 6,  7,  8},
    {9, 10, 11, 12}
  };

  // pointer ptr pointing at array num
  int *ptr = &num[0][0];
  
  // other variables
  int
    ROWS = 3,
    COLS = 4,
    TOTAL_CELLS = ROWS * COLS,
    i;
  
  // print the elements of the array num via pointer ptr
  for (i = 0; i < TOTAL_CELLS; i++) {
    printf("%d ", *(ptr + i));
  }
  
  return 0;
}

Output:

1 2 3 4 5 6 7 8 9 10 11 12

Address mapping

We can compute the address of an element of the array by using the rows and columns of the array. For this we use the following formula.

arr[i][j] = baseAddress + [(i x no_of_cols + j) x size_of_data_type]

Where, arr is a two dimensional array. i and j denotes the ith row and jth column of the array.

baseAddress denotes the address of the first element of the array. And no_of_cols is the total number of columns in the row.

And size_of_data_type is the size of the type of the pointer. If the type is int then size_of_data_type = 2 bytes and if the type is char then size_of_data_type = 1 bytes.

For example, in the case of num array the baseAddress = 1000, no_of_cols = 4 and size_of_data_type = 2.

So, we can compute the memory address location of the element num[2][3] as follows.

// address of element at cell 2,3
num[2][3] = baseAddress + [(i x no_of_cols + j) x size_of_data_type]
          = 1000 + [(2 x 4 + 3) x 2]
          = 1000 + [(8 + 3) x 2]
          = 1000 + 22
          = 1022

Accessing the value of the two dimensional array via pointer using row and column of the array

If we want to get the value at any given row, column of the array then we can use the value at the address of * operator and the following formula.

arr[i][j] = *(ptr + (i x no_of_cols + j))

Where, arr is a two dimensional array and i and j denotes the ith row and jth column of the array.

ptr holds the address of the first element of the array.

And no_of_cols denotes the total number of column in the row of the array.

In the following example we are finding the value at the location 2nd row and 3rd column of the array num.

// value at num[2][3] where, i = 2 and j = 3
num[2][3] = *(ptr + (i x no_of_cols + j))
          = *(ptr + (2 x 4 + 3))
          = *(ptr + 11)

Complete code

#include <stdio.h>

int main(void) {
  
  // 2d array
  int num[3][4] = {
    {1, 2,  3,  4},
    {5, 6,  7,  8},
    {9, 10, 11, 12}
  };
  
  int
    ROWS = 3,
    COLS = 4,
    i, j;

  // pointer
  int *ptr = &num[0][0];
  
  // print the element of the array via pointer ptr
  for (i = 0; i < ROWS; i++) {
    for (j = 0; j < COLS; j++) {
      printf("%d ", *(ptr + i * COLS + j));
    }
    printf("\n");
  }
  
  return 0;
}

Output:

1 2 3 4
5 6 7 8
9 10 11 12