Propositional Logic Truth Table

In this tutorial we will learn about truth table.

Introduction to Propositional Logic, types of propositions and the types of connectives are covered in the previous tutorial.

Truth values

Every proposition (simple or compound) will take one of the two values true or false and these values are called the truth values.

We denote the value true as 1 and value false as 0.

Truth value is defined as the truth or falsity of a proposition.

All proposition will have a truth value (i.e., they are either true or false)

Truth Value of Simple Proposition

Consider the following simple proposition.

2 is greater than 1

The truth value of the proposition is TRUE.

Consider another simple proposition.

The word Mango comes before the word Apple in Oxford Dictionary.

The truth value of the proposition is FALSE this is because M comes after A.

Truth Value of Compound Proposition

The truth value of a compound proposition can be figured out based on the truth values of its components.

Consider the following compound proposition.

October 21, 2012 was Sunday and Sunday is a holiday.

The given compound proposition is made up of two simple propositions
,
p = October 21, 2012 was Sunday
q = Sunday is a holiday

Remember! we can denote propositions using small letters like a,b,c... p,q,r... etc

If we check 2012 calendar, 21st October was Sunday. So, truth value of the simple proposition p is TRUE.

Sunday is a holiday. So, the truth value of the simple proposition q is TRUE.

So, p = TRUE and q = TRUE.

We started with the following compound proposition "October 21, 2012 was Sunday and Sunday is a holiday".

Note the word and in the statement. It is joining the two simple propositions into a compound proposition.

So, we can write
x = p AND q
where, x is the compound proposition created by joining the two simple proposition p and q using the conjunctive operator AND.

The truth value of x will be TRUE only when both p and q are TRUE because we are using the conjunctive operator (also called AND).

Note! if any one of them is FALSE then truth value of x will be FALSE.

We know that the truth value of both the simple proposition p and q is TRUE.
So, we can write
x = p AND q
= TRUE AND TRUE
= TRUE

So, the truth value of the compound proposition x = TRUE.

Therefore, the truth value of a compound proposition can be figured out based on the
truth values of its components.

Truth Table

A truth table is a complete list of possible truth values of a given proposition.

So, if we have a proposition say p. Then its possible truth values are TRUE and FALSE because a proposition can either be TRUE or FALSE and nothing else. And we can draw the truth table for p as follows.

Note! we can denote value TRUE
using T and 1 and value FALSE using F and 0.

Number of rows in a Truth Table

There is a formula to calculate the total number of rows in the truth table for a given number of propositions for all possible truth values combination.

We know that we can denote proposition using small letters like p, q, r, ... etc and we also know that a proposition (simple or compound) can either be TRUE or FALSE and nothing else.

So, if we have 1 proposition (say p) then, total possible truth values of p = 2
i.e., 2¹ = 2

Similarly, if we have 2 propositions (say p and q).
Then, all possible truth values = 2² = 4

Similarly, if we have 3 propositions (say p, q and r)
Then, all possible truth values = 2³ = 8

Truth tables of the logical connectives (operators)

Types of Logical Connectives (Operators)

• Negation (also called NOT)
• Disjunctive (also called OR)
• Conjunctive (also called AND)
• Conditional (also called Implication)
• Bi-conditional (also called Equivalence)

Negation (also called NOT)

The negation operator simply inverse the truth value of a proposition. This is the only operator that works on a single proposition and hence is also called a unary connective (operator).

If p is a proposition then its negation is denoted by ~p or p'.

So, if p is true then, NOT p i.e., ~p = false. Similarly, if p is false then, ~p = true.

Following is the truth table for the negation operator

Disjunctive (also called OR) operator

The OR connective (operator) works with two or more propositions.

The disjunctive of p and q propositions is denoted by
p + q
p ∨ q
And the result of p + q is true only when p is true, or q is true or both are true.

Truth table for disjunctive (OR operator) for the two propositions

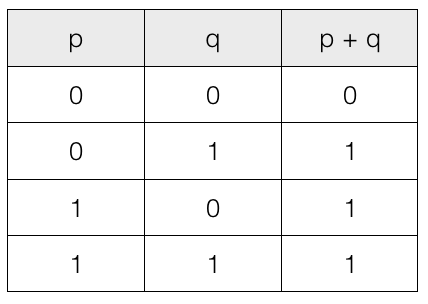
Note! If one of the proposition is 1 (true) then output is 1 (true).

Conjunctive (also called AND) operator

The AND connective (operator) works with two or more propositions.

The conjunctive of p and q propositions is denoted by
p . q
p ∧ q
and the result of p . q is true only when both are true.

Truth table for conjunctive (AND operator) for the two propositions

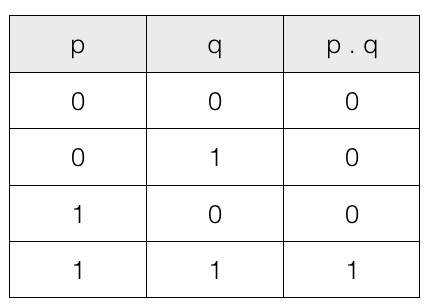
Note! If both propositions are 1 (true) then output is 1 (true).

Conditional (also called Implication) operator

The conditional operator is also called implication (If...Then). The conditional p ⇒ q is false when p is true and q is false and for all other input combination the output is true.

The proposition p and q can themselves be simple and compound propositions. The first part p is called the antecedent and the second part q is called the consequent.

The conditional p ⇒ q can be expressed as p ⇒ q = ~p + p

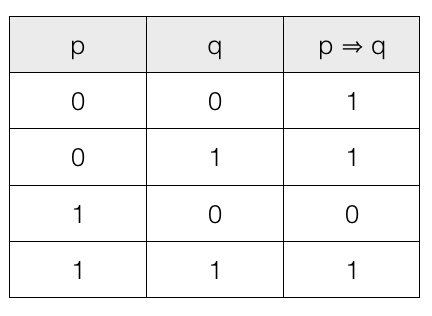
Truth table for conditional p ⇒ q
For conditional, if p is true and q is false then output is false and for all other input combination it is true.

We can also express conditional p ⇒ q = ~p + q
Lets check the truth table.

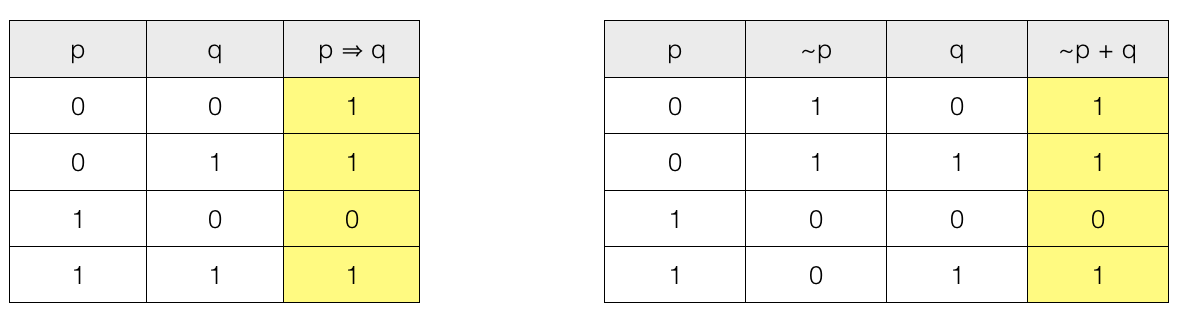
We can see that the result p ⇒ q and ~p + q are same.

Bi-conditional (also called Equivalence) operator

The bi-conditional operator is also called equivalence (If and only If). The bi-conditional p ⇔ q is false when one proposition is true and the other is false and for all other input combination the output is true.

The proposition p and q can themselves be simple and compound propositions.

The bi-conditional can be expressed as p ⇔ q = (p . q) + (~p . ~q)

Truth table for bi-conditional p ⇔ q
For bi-conditional, if one proposition is true and the other is false then output is false. For all other input combination it is true.

We can also express bi-conditional p ⇔ q = (p . q) + (~p . ~q)
lets check the truth table

We can see that the result p ⇔ q and (p . q) + (~p . ~q) are same.

And this brings us to the end of this tutorial.