Problem on Trains
Aptitude
Important notes and formula
Convert km/hr to m/s
| N km/hr = | N x | 5 | m/s | ||
| 18 |
Convert m/s to km/hr
| N m/s = | N x | 18 | km/hr | ||
| 5 |
Crossing a pole
Time taken by a train of length L meters to cross a person standing on a platform, or a signal pole or a lamp post is equal to the time taken by the train to cover L meters. 
Crossing an object or platform
Time taken by a train of length L meters to cross a platform or object of length X is equal to the time taken by the train to cover (L + X) meters. 
Two trains running in opposite direction
If two trains are running in opposite direction at a speed u m/s and v m/s respectively then their relative speed is (u+v) m/s. 
Two trains running in same direction
If two trains are running in same direction at a speed u m/s and v m/s respectively then their relative speed is (u-v) m/s where, u > v. 
Two trains running in opposite direction (case 2)
If two trains L meters and M meters are running in opposite direction at a speed u m/s and v m/s respectively.
Then time taken by the trains to cross each other is
(L + M) / (u + v) seconds. 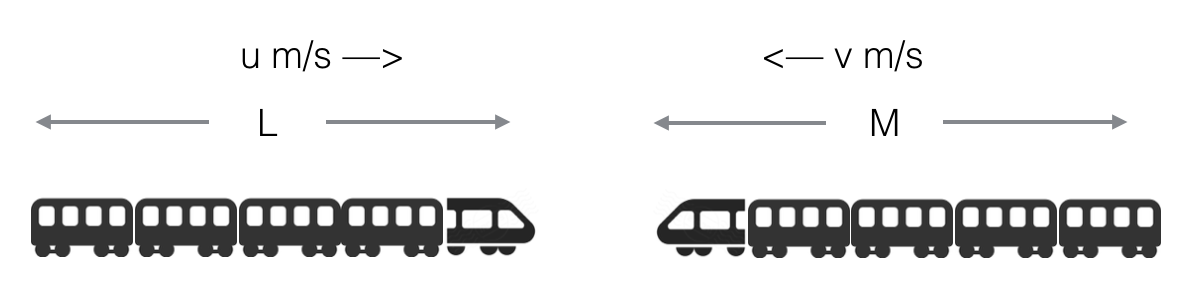
Two trains running in same direction (case 2)
If two trains L meters and M meters are running in same direction at a speed u m/s and v m/s respectively where, u > v.
Then time taken by the faster train to cross the slower train is
(L + M) / (u - v) seconds. 
Finding speed
If two trains start from point A and B respectively at the same time and starts approaching each other and after crossing they take x and y seconds respectively to reach point B and A respectively. Then speed of the two trains will be
u : v = √x : √y 
ADVERTISEMENT